SIFT理论与概述
参考 首先简要介绍SIFT原理和实现过程,本文不涉及严格详细的数学推导,如有需要请参阅原文。
SIFT是一种特征点识别算法,是Scale-Invariant Feature Transform的缩写。SIFT识别的特征点由图像的宽度、高度和尺度三个维度唯一确定。通过引入尺度特征,SIFT得到的特征点更加鲁棒。这里的鲁棒是指,一定程度上,即使目标模板改变尺寸,图像质量变好或降低,模板视点、宽高比发生变化时,SIFT依然可以捕获相同的特征点。SIFT所提取的关键点包含了位置和方向两种信息,主方向的引入使得SIFT具备旋转不变性。 通过统计特征点邻域像素的梯度直方图,SIFT为每个特征点生成一个128维的描述向量。描述子使得特征点之间可以进行比较,从而使SIFT可以被应用到许许多多下游任务中,成为计算机视觉邻域的重要方法。
SIFT的实现可以简述为以下三个步骤:首先由输入图像生成尺度空间高斯差分图像金字塔,然后从图像金字塔中识别出特征点,最后为每一个特征点生成一个描述子。对输入图像进行一系列的高斯模糊和降采样操作,生成高斯图像金字塔,同层金字塔的相邻高斯图像进行差分操作生成高斯差分图像金字塔。高斯差分图像中,每个尺度空间的像素点与其26邻域像素进行比较,若该像素点为极值点,则将其加入特征点集。对每个特征点,计算统计其邻域梯度直方图得到主方向。若其它方向上的梯度权重大于主方向梯度权重的80%时,认为该方向也起重要作用。每个方向对应一个特征点,此时,将上述特征点的位置信息赋给该方向,生成一个新的特征点。最后,根据特征点的邻域像素分布为每个特征点生成一个128维的向量,即描述子。整个SIFT算法流程可由下面的函数表示。
def computeKeypointsAndDescriptors(image,sigma=1.6,num_intervals=3,assumed_blur=0.5,image_border_width=5):
"""
Compute SIFT keypoints and descriptors for an image
:param image:
:param sigma:
:param num_intervals:
:param assumed_blur:
:param image_border_width:
:return:
"""
image = image.astype('float32')
base_image = generateBaseImage(image,sigma,assumed_blur)
num_octaves = computeNumberOfOctaves(base_image.shape)
gaussian_kernels = generateGaussianKernels(sigma,num_intervals)
gaussian_images = generateGaussianImages(base_image,num_octaves,gaussian_kernels)
dog_images = generateDoGImages(gaussian_images)
keypoints = findScaleSpaceExtrema(gaussian_images,dog_images,num_intervals,sigma,image_border_width)
keypoints = removeDuplicateKeypoints(keypoints)
keypoints = convertKeypointsToInputImageSize(keypoints)
descriptors = generateDescriptors(keypoints,gaussian_images)
return keypoints,descriptors
再次说明,SIFT中许多晦涩的细节大多与尺度空间有关,比如如何确定高斯模糊的尺度、如何将特征点从一个尺度转换到另一个尺度等,本文并不涉及这些细节的详细推导严格证明,具体请参阅原文。
尺度空间和图像金字塔
生成图像金字塔的基始图像
为了更好的利用原图像的原始信息,简单的将原图像的尺寸扩大2倍并对其进行高斯模糊平滑,以此作为高斯图像金字塔的基始图像。假设输入图像有assumed_blur的模糊度,为了使我们获得的基始图像有sigma的模糊值,需要对尺寸扩大了一倍的图像进行模糊值为sigma_diff的高斯模糊操作。 assumed_blur、sigma和sigma_diff三者存在如下关系:
sigma^2 = assumed_blur^2 + sigma_diff^2. (1)
详细的证明请参阅此文
def generateBaseImage(image,sigma,assumed_blur):
"""
Generate base image from input image by upsampling by 2 in both directions and blurring
:param image:
:param sigma:
:param assumed_blur:
:return:
"""
logger.debug('Generating base image ...')
image = resize(image,(0,0),fx=2,fy=2,interpolation=INTER_LINEAR)
sigma_diff = sqrt(max((sigma**2)-((2*assumed_blur)**2),0.01))
return GaussianBlur(image,(0,0),sigmaX=sigma_diff,sigmaY=sigma_diff)

计算图像金字塔的层数
生成图像金字塔的过程中,我们不断重复对图像进行下采样,使得每一层的图像尺寸每次减小为上一层的一半,直到图像尺寸小到不能再降采样。则金字塔的层数octave满足:
2^octave = min(image_shape)
在实际中金字塔的层数最多为octave-1,因为在检测特征点的时是在3×3×3的尺度子空间中进行的。
def computeNumberOfOctaves(image_shape):
"""
Compute number of octaves in image pyramid
:param image_shape:
:return:
"""
return int(round(log(min(image_shape))/log(2)-1))
生成高斯核
假设图像金字塔一共有numOvtaves层,每层有numIntervals+3张图像。每一层的图像都有相同的长度和宽度,图像的模糊层度是逐渐增加的。经过numIntervals次逐步高斯模糊,图像的blur值变为了原来的两倍,同时生成了numIntervals+1张图像。高斯差分金字塔图像由相邻的高斯模糊图像做差分得到,因此我们还需要额外生成两张高斯模糊图像以使得到相同数量的高斯差分图。容易想到这两张额外的高斯模糊图分别位于上述numIntervals+1张高斯模糊图的第一张之前和最后一张之后,故每层金字塔一共numIntervals+3张图像。下面的函数计算出对应的高斯核大小,用于生成高斯图像金字塔。根据sift原文中提供的sigma和num_intervals初值,可以得到如下的高斯核序列:
array([1.6,1.22627,1.54501,1.94659,2.45255,1.09002])
根据公式(1),容易算出每层图像实际的高斯模糊值分别为:
array([1.6 ,2.01587,2.53984,3.2,4.03175,5.07969])
可以看到array[-3]刚好是array[0]的两倍,故我们对每层金字塔的倒数第三张图进行下采样,作为下一层金字塔的输入图像。
def generateGaussianKernels(sigma,num_intervals):
"""
Generate list of gaussian kernels at which to blur the input image
:param sigma:
:param num_intervals:
:return:
"""
logger.debug('Generating scales...')
num_images_per_octave = num_intervals + 3
k = 2 ** (1. / num_intervals)
gaussian_kernels = zeros(num_images_per_octave)
gaussian_kernels[0] = sigma
for image_index in range(1,num_images_per_octave):
sigma_previous = (k**(image_index-1))*sigma
sigma_total = k * sigma_previous
gaussian_kernels[image_index] = sqrt(sigma_total**2 - sigma_previous**2)
return gaussian_kernels
生成高斯图像金字塔
生成高斯图像金字塔的过程相对简单,执行一系列下采样、高斯模糊的操作即可,其中需要注意的是:
- 每层高斯金字塔的第一张图像已经有了相应的高斯模糊值,故跳过kernels序列的第一个元素。
- 每层高斯金字塔的倒数第三张图降采样处理后作为下一层高斯金字塔的第一张图。
def generateGaussianImages(image,num_octaves,gaussian_kernels):
"""
Generate scale-space pyramid of Gaussian images
:param image:
:param num_octaves:
:param gaussian_kernels:
:return:
"""
logger.debug('Generating Gaussian images...')
gaussian_images = []
for octave_index in range(num_octaves):
gaussian_images_in_octave = []
gaussian_images_in_octave.append(image)
for gaussian_kernel in gaussian_kernels[1:]:
image = GaussianBlur(image,(0,0),sigmaX=gaussian_kernel,sigmaY=gaussian_kernel)
gaussian_images_in_octave.append(image)
gaussian_images.append(gaussian_images_in_octave)
octave_base = gaussian_images_in_octave[-3]
image = resize(octave_base,(int(octave_base.shape[1]/2),int(octave_base.shape[0]/2)),interpolation=INTER_NEAREST)
return array(gaussian_images,dtype=object)
生成差分图像金字塔
对高斯图像金字塔中每层的相邻图像进行差分操作,获得该层的高斯差分图像。由此生成了尺度空间的高斯差分图像金字塔。
def generateDoGImages(gaussian_images):
"""
Generate Difference-of-Gaussians image pyramid
:param gaussian_images:
:return:
"""
logger.debug('Generating Difference-of-Gaussian images...')
dog_images = []
for gaussian_images_in_octave in gaussian_images:
dog_images_in_octave = []
for first_image,second_image in zip(gaussian_images_in_octave,gaussian_images_in_octave[1:]):
dog_images_in_octave.append(subtract(second_image,first_image))
dog_images.append(dog_images_in_octave)
return array(dog_images,dtype=object)
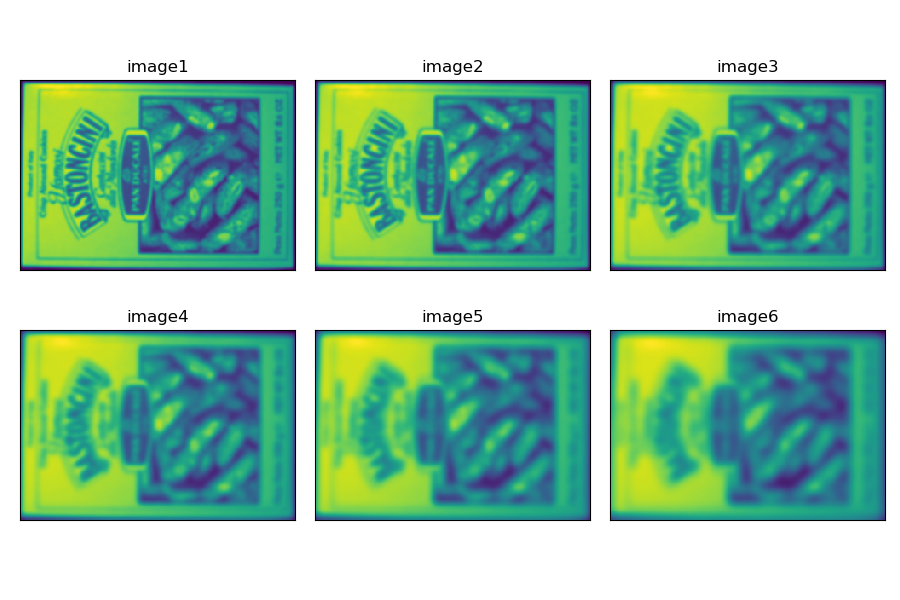

特征点提取
尺度空间的特征点提取可简单分为以下两步:
- 寻找极值点,并通过二次拟合将极值点定位到亚像素级别。
- 计算每个极值点的主方向,生成特征点。
求解极值点
由于每层金字塔中的图像尺寸大小都相同,只是模糊程度不一样,故只需每次提取三张图像,对每层进行迭代求解,寻找极值点即可。对每个三张图像组,判断位于最中间的像素点值是否大于或小于其26邻域的像素点值。若条件成立则该点是一个极值点。这里的26邻域点分别是指:中间层图像中的8邻域点,以及上下两张图像中分别对应的9个点,即26=8+9+9。
def isPixelAnExtremum(first_subimage,second_subimage,third_subimage,threshold):
"""
Return true if the center element of the 3×3×3 input array is strictly greater than or less than all its neighbors, False otherwise
:param first_subimage:
:param second_subimage:
:param third_subimage:
:param threshold:
:return:
"""
center_pixel_value = second_subimage[1,1]
if abs(center_pixel_value) > threshold:
if center_pixel_value > 0 :
return all(center_pixel_value>=first_subimage) and all(center_pixel_value>=third_subimage) and all(center_pixel_value>=second_subimage[0,:]) and all(center_pixel_value >= second_subimage[2,:]) and center_pixel_value>=second_subimage[1,0] and center_pixel_value >= second_subimage[1,2]
elif center_pixel_value < 0:
return all(center_pixel_value <= first_subimage) and all(center_pixel_value <= third_subimage) and all(center_pixel_value <= second_subimage[0, :]) and all(center_pixel_value <= second_subimage[2, :]) and center_pixel_value <= second_subimage[1, 0] and center_pixel_value <= second_subimage[1, 2]
return False
二次拟合定位
为了使特征点的位置信息更加准确,需要对求得的极值点进行拟合操作。通过一个二次模型来拟合输入极值点和其对应的26邻域,然后根据拟合的模型得到亚像素级别的极值估计,逐次逼近更新极值点的位置,直到收敛。具体实现中,通过最多5次迭代,若极值点任意一个维度的改变量小于0.5,认为二次模型收敛到该极值点。二次模型拟合过程中需要计算极值点的梯度和Hessian矩阵,由于像素点是离散值,故使用二阶中心有限差分来近视。 辅助函数computeGradientAtCenterPixel()和computeHessianAtCenterPixel()分别实现极值点梯度和Hessian矩阵的求解。
def localizeExtremumViaQuadraticFit(i,j,image_index,octave_index,num_intervals,dog_images_in_octave,sigma,contrast_threshold,image_border_width,eigenvalue_ratio=10,num_attempts_until_convergence=5):
"""
Iteratively refine pixel positions of scale-space extrema via quadratic fit around each extrema's neighbors.
:param i:
:param j:
:param image_index:
:param octave_index:
:param num_intervals:
:param dog_images_in_octave:
:param sigma:
:param contrast_threshold:
:param image_border_width:
:param eigenvalue_ratio:
:param num_attempts_until_convergence:
:return:
"""
logger.debug('Localizing scale-space extrema...')
extremum_is_outside_image = False
image_shape = dog_images_in_octave[0].shape
for attempt_index in range(num_attempts_until_convergence):
first_image,second_image,third_image = dog_images_in_octave[image_index-1:image_index+2]
pixel_cube = stack([first_image[i-1:i+2,j-1:j+2],second_image[i-1:i+2,j-1:j+2],third_image[i-1:i+2,j-1:j+2]]).astype('float32')/255.
gradient = computeGradientAtCenterPixel(pixel_cube)
hessian = computeHessianAtCenterPixel(pixel_cube)
extremum_update = -lstsq(hessian,gradient,rcond=None)[0]
if abs(extremum_update[0])<0.5 and abs(extremum_update[1])<0.5 and abs(extremum_update[2])<0.5:
break
j += int(round(extremum_update[0]))
i += int(round(extremum_update[1]))
image_index += int(round(extremum_update[2]))
if i < image_border_width or i >= image_shape[0]-image_border_width or j < image_border_width or j >= image_shape[1] - image_border_width or image_index < 1 or image_index > num_intervals:
extremum_is_outside_image = True
break
if extremum_is_outside_image:
logger.debug('Update extremum moved outside of image before reaching convergence. Skipping...')
return None
if attempt_index >= num_attempts_until_convergence-1:
logger.debug('Exceeded maximum number of attempts without reaching convergence for this extremum. Skipping...')
return None
functionValueAtUpdatedExtremum = pixel_cube[1,1,1] + 0.5 * dot(gradient,extremum_update)
if abs(functionValueAtUpdatedExtremum)*num_intervals >= contrast_threshold:
xy_hessian = hessian[:2,:2]
xy_hessian_trace = trace(xy_hessian)
xy_hessian_det = det(xy_hessian)
if xy_hessian_det >0 and eigenvalue_ratio * (xy_hessian_trace**2)<((eigenvalue_ratio+1)**2)*xy_hessian_det:
keypoint = KeyPoint()
keypoint.pt = ((j+extremum_update[0])*(2**octave_index),(i+extremum_update[1])*(2**octave_index))
keypoint.octave = octave_index + image_index*(2**8)+int(round((extremum_update[2]+0.5)*255))*(2**16)
keypoint.size = sigma*(2**((image_index+extremum_update[2])/float32(num_intervals)))*(2**(octave_index+1))
keypoint.response = abs(functionValueAtUpdatedExtremum)
return keypoint,image_index
return None
def computeGradientAtCenterPixel(pixel_array):
"""
Approximate gradient at center pixel [1,1,1] of 3×3×3 array using central difference formula of order O(h^2),where h is step size
f'(x) = (f(x+h)-f(x-h))/(2*h)
:param pixel_array:
:return:
"""
dx = 0.5 * (pixel_array[1,1,2]-pixel_array[1,1,0])
dy = 0.5 * (pixel_array[1,2,1]-pixel_array[1,0,1])
dz = 0.5 * (pixel_array[2,1,1]-pixel_array[0,1,1])
return array([dx,dy,dz])
def computeHessianAtCenterPixel(pixel_array):
"""
Approximate Hessian at center pixel [1,1,1] of 3×3×3 array using central difference formula of order O(h^2), where h is the step size
f''(x) = (f(x+h)-2*f(x)+f(x-h))/(h^2)
d''(f(x,y))/dxdy = (f(x+h,y+h)-f(x+h,y-h)-f(x-h,f+h)+f(x-h,y-h))/(4*h^2)
:param pixel_array:
:return:
"""
center_pixel_value = pixel_array[1,1,1]
dxx = pixel_array[1,1,2]-2*center_pixel_value+pixel_array[1,1,0]
dyy = pixel_array[1,2,1]-2*center_pixel_value+pixel_array[1,0,1]
dss = pixel_array[2,1,1]-2*center_pixel_value+pixel_array[0,1,1]
dxy = 0.25 * (pixel_array[1,2,2]-pixel_array[1,2,0]-pixel_array[1,0,2]+pixel_array[1,0,0])
dxs = 0.25 * (pixel_array[2,1,2]-pixel_array[2,1,0]-pixel_array[0,1,2]+pixel_array[0,1,0])
dys = 0.25 * (pixel_array[2,2,1]-pixel_array[0,2,1]-pixel_array[2,0,1]+pixel_array[0,0,1])
return array([[dxx,dxy,dxs],[dxy,dyy,dys],[dxs,dys,dss]])
主方向求解
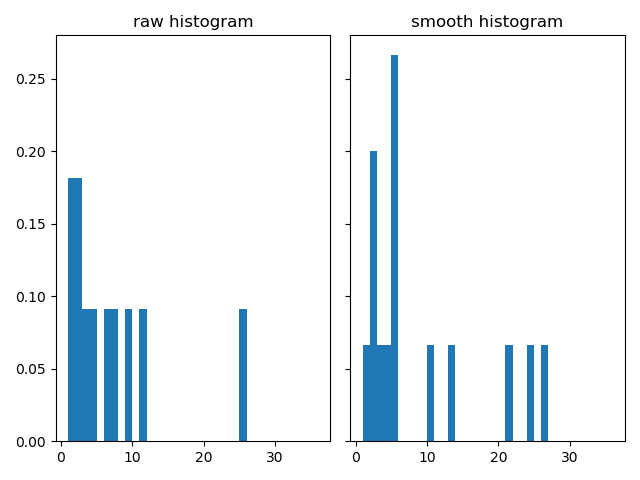
首先为特征点附近的像素点创建一个梯度直方图,然后对直方图进行拟合平滑,最后选取直方图中柱值最大的一项作为关键点的主方向。SIFT指出,当直方图中的某一项大于主方向对应幅值的80%时,不可将该方向忽略。值得注意的时,这里的邻域像素点是指以关键点为圆心,半径为3sigma的圆内的点。从概率角度来说,这意味着直方图的计算统计包含了影响关键点权重99.7%的像素点。 以特征点为圆心将邻域空间分为36组,每组对应10度。即直方图有36柱,每柱的高低由该柱对应方向区间内的像素点梯度决定。具体来说,分别求解每个像素点的梯度大小和方向,方向指示该像素点位于哪一组,即直方图中的哪一柱,然后将梯度大小的加权值累加到相应的柱上。这里的加权可简单理解为,离关键点越远的像素点权重越小,表示对关键点的影响越小。获得原始梯度直方图后,对直方图进行平滑处理。这里的平滑因子等价与一个5点高斯滤波核,详细的推导请参考此处 。 然后在平滑后的直方图中查找满足条件的方向,为每个方向创建一个关键点。
def computeKeypointsWithOrientations(keypoint,octave_index,gaussian_image,radius_factor=3,num_bins=36,peak_ratio=0.8,scale_factor=1.5):
"""
compute orientations for each keypoint
:param keypoint:
:param octave_index:
:param gaussian_image:
:param radius_factor:
:param num_bins:
:param peak_ratio:
:param scale_factor:
:return:
"""
logger.debug('Computing keypoint orientations...')
keypoints_with_orientations = []
image_shape = gaussian_image.shape
scale = scale_factor*keypoint.size/float32(2**(octave_index+1))
radius = int(round(radius_factor*scale))
weight_factor = -0.5 /(scale**2)
raw_histogram = zeros(num_bins)
smooth_histogram = zeros(num_bins)
for i in range(-radius,radius+1):
region_y = int(round(keypoint.pt[1]/float32(2**octave_index))) + i
if region_y>0 and region_y < image_shape[0]-1:
for j in range(-radius,radius+1):
region_x = int(round(keypoint.pt[0]/float32(2**octave_index)))+j
if region_x > 0 and region_x < image_shape[1]-1:
dx = gaussian_image[region_y,region_x+1]-gaussian_image[region_y,region_x-1]
dy = gaussian_image[region_y-1,region_x]-gaussian_image[region_y+1,region_x]
gradient_magnitude = sqrt(dx*dx + dy*dy)
gradient_orinetation = rad2deg(arctan2(dy,dx))
weight = exp(weight_factor * (i**2 + j**2))
histogram_index = int(round(gradient_orinetation*num_bins/360.))
raw_histogram[histogram_index%num_bins] += weight * gradient_magnitude
for n in range(num_bins):
smooth_histogram[n] = (6*raw_histogram[n] + 4*(raw_histogram[n-1] + raw_histogram[(n+1)%num_bins])+raw_histogram[n-2]+raw_histogram[(n+2)%num_bins])/16
orientation_max = max(smooth_histogram)
orientation_peaks = where(logical_and(smooth_histogram>roll(smooth_histogram,1),smooth_histogram>roll(smooth_histogram,-1)))[0]
for peak_index in orientation_peaks:
peak_value = smooth_histogram[peak_index]
if peak_value >= peak_ratio * orientation_max:
left_value = smooth_histogram[(peak_index-1)%num_bins]
right_value = smooth_histogram[(peak_index+1)%num_bins]
interpolated_peak_index = (peak_index + 0.5*(left_value-right_value)/(left_value-2 * peak_value+right_value))%num_bins
orientation = 360. - interpolated_peak_index*360./num_bins
if abs(orientation-360)<float_tolerance:
orientation = 0
new_keypoint = KeyPoint(*keypoint.pt,keypoint.size,orientation,keypoint.response,keypoint.octave)
keypoints_with_orientations.append(new_keypoint)
return keypoints_with_orientations
特征点求解和清洗
通过在尺度空间求解极值点的位置信息和方向信息后,我们得到了一系列的特征点集。在为其生成描述子之前,我们需要对特征点进行清洗和转换: a. 清洗主要目的为移除重复的特征点, b. 转换是指将特征点从baseImage坐标变换到原始输入图像坐标中。 目前为止,我们已经求解出了特征点。
def findScaleSpaceExtrema(gaussian_images,dog_images,num_intervals,sigma,image_border_width,contrast_threshold=0.04):
"""
find pixel positions of all scale-space extrema in the image pyramid
:param gaussian_images:
:param dog_images:
:param num_intervals:
:param sigma:
:param image_border_width:
:param contrast_threshold:
:return:
"""
logger.debug('Find scale-space extrema...')
threshold = floor(0.5 * contrast_threshold / num_intervals * 255) # follow OpenCV convention
keypoints = []
for octave_index,dog_images_in_octave in enumerate(dog_images):
for image_index,(first_image,second_image,third_image) in enumerate(zip(dog_images_in_octave,dog_images_in_octave[1:],dog_images_in_octave[2:])):
for i in range(image_border_width,first_image.shape[0]-image_border_width):
for j in range(image_border_width,first_image.shape[1]-image_border_width):
if isPixelAnExtremum(first_image[i-1:i+2,j-1:j+2],second_image[i-1:i+2,j-1:j+2],third_image[i-1:i+2,j-1:j+2],threshold):
localization_result = localizeExtremumViaQuadraticFit(i,j,image_index+1,octave_index,num_intervals,dog_images_in_octave,sigma,contrast_threshold,image_border_width)
if localization_result is not None:
keypoint,localized_image_index = localization_result
keypoints_with_orientations = computeKeypointsWithOrientations(keypoint,octave_index,gaussian_images[octave_index][localized_image_index])
for keypoints_with_orientation in keypoints_with_orientations:
keypoints.append(keypoints_with_orientation)
return keypoints
def removeDuplicateKeypoints(keypoints):
"""
Sort keypoints and remove duplicate keypoints
:param keypoints:
:return:
"""
if len(keypoints) < 2:
return keypoints
keypoints.sort(key=cmp_to_key(compareKeypoints))
unique_keypoints = [keypoints[0]]
for next_keypoint in keypoints[1:]:
last_unique_keypoint = unique_keypoints[-1]
if last_unique_keypoint.pt[0] != next_keypoint.pt[0] or last_unique_keypoint.pt[1] != next_keypoint.pt[1] or last_unique_keypoint.size != next_keypoint.size or last_unique_keypoint.angle != next_keypoint.angle:
unique_keypoints.append(next_keypoint)
return unique_keypoints
def compareKeypoints(keypoint1,keypoint2):
"""
Return true is keypoint1 is less than keypoint2
:param keypoint1:
:param keypoint2:
:return:
"""
if keypoint1.pt[0] != keypoint2.pt[0]:
return keypoint1.pt[0] - keypoint2.pt[0]
if keypoint1.pt[1] != keypoint2.pt[1]:
return keypoint1.pt[1] - keypoint2.pt[1]
if keypoint1.size != keypoint2.size:
return keypoint2.size - keypoint1.size
if keypoint1.angle != keypoint2.angle:
return keypoint1.angle -keypoint2.angle
if keypoint1.response != keypoint2.response:
return keypoint2.response - keypoint1.response
if keypoint1.octave != keypoint2.octave:
return keypoint2.octave - keypoint1.octave
return keypoint2.class_id - keypoint1.class_id
def convertKeypointsToInputImageSize(keypoints):
"""
Convert keypoint point, size, and octave to input image size
:param keypoints:
:return:
"""
convert_keypoints = []
for keypoint in keypoints:
keypoint.pt = tuple(0.5*array(keypoint.pt))
keypoint.size *= 0.5
keypoint.octave = (keypoint.octave & ~255) | ((keypoint.octave - 1) & 255)
convert_keypoints.append(keypoint)
return convert_keypoints

描述子生成
描述子编码了特征点的邻域信息,使得特征点之间可以被比较。SIFT描述子经过精心设计,可实现鲁棒的特征点匹配。 对于每一个特征点,首先创建一个梯度直方图。考虑特征点的平方邻域,将该邻域内的点旋转与特征点角度相同的度数,即让该正方形邻域的长轴与特征点的主方向相同,该操作使得SIFT具备旋转不变性。然后计算行柱和列柱下标,该索引用于定位邻域点。计算每个像素点的梯度大小和方向,与求取特征点的主方向不同,这里仅仅记录每个像素点的直方图柱索引和柱值,而不是立马计算统计出梯度直方图。同时需要注意的是,这里的直方图为8个柱,每个柱覆盖45度。用一个2维矩阵表示领域像素,用一个8维向量表征一个像素点。每个像素点的方向柱索引对应向量相应的下标,该下标对应的空间存储该方向的加权梯度值。这样我们形成了一个大小为邻域宽度×邻域宽度×直方图柱数的3D矩阵,最后将该3D向量扁平化为一个一维向量,即得到该特征点对应的SIFT描述子。 值得注意的是,在扁平化之前,需要进行一步平滑操作。将每个像素的加权梯度值从行柱、列柱、方向柱三个维度分配给其8邻域点。简单来说,每个邻域像素点有相应的行索引、列索引和方向索引,我们想要将其直方图上对应的值以恰当的方式分配给8个邻域点,并且确保其分配的值可以还原出被分配的梯度值。可以想象为将正方体内的一个像素点值分配给正方体8个顶点上的像素,由于被分配的像素点并不一定位于正方体的中心,故不能简单地均分。这里采用三线性插值函数的反函数实现分配,具体数学推导请参阅此处。经过平滑后,将3D矩阵压缩为一个128维的向量,然后进行归一化和滤值处理,使得描述子中元素值域为0到255,便于其他操作。
def generateDescriptors(keypoints,gaussian_images,window_width=4,num_bins=8,scale_multiplier=3,descriptor_max_value=0.2):
"""
Generate descriptor for each keypoint
:param keypoints:
:param gaussian_images:
:param window_width:
:param num_bins:
:param scale_multiplier:
:param descriptor_max_value:
:return:
"""
logger.debug('Generating descriptors...')
descriptors = []
for keypoint in keypoints:
octave,layer,scale = unpackOctave(keypoint)
gaussian_image = gaussian_images[octave+1,layer]
num_rows,num_cols = gaussian_image.shape
point = round(scale*array(keypoint.pt)).astype('int')
bins_per_degree = num_bins/360.
angle = 360. - keypoint.angle
cos_angle = cos(deg2rad(angle))
sin_angle = sin(deg2rad(angle))
weight_multiplier = -0.5 / ((0.5*window_width)**2)
row_bin_list = []
col_bin_list = []
magnitude_list = []
orientation_bin_list = []
histogram_tensor = zeros((window_width+2,window_width+2,num_bins))
hist_width = scale_multiplier * 0.5 * scale * keypoint.size
half_width = int(round(hist_width*sqrt(2)*(window_width+1)*0.5))
half_width = int(min(half_width,sqrt(num_rows**2 + num_cols**2)))
for row in range(-half_width,half_width+1):
for col in range(-half_width,half_width+1):
row_rot = col * sin_angle + row * cos_angle
col_rot = col * cos_angle + row * sin_angle
row_bin = (row_rot/hist_width) + 0.5*window_width - 0.5
col_bin = (col_rot/hist_width) + 0.5*window_width - 0.5
if row_bin > -1 and row_bin < window_width and col_bin > -1 and col_bin < window_width:
window_row = int(round(point[1]+row))
window_col = int(round(point[0]+col))
if window_row > 0 and window_row < num_rows-1 and window_col > 0 and window_col < num_cols-1:
dx = gaussian_image[window_row,window_col+1] - gaussian_image[window_row,window_col-1]
dy = gaussian_image[window_row-1,window_col] - gaussian_image[window_row+1,window_col]
gradient_magnitude = sqrt(dx*dx+dy*dy)
gradient_orientation = rad2deg(arctan2(dy,dx))%360
weight = exp(weight_multiplier*((row_rot/hist_width)**2+(col_rot/hist_width)**2))
row_bin_list.append(row_bin)
col_bin_list.append(col_bin)
magnitude_list.append(weight*gradient_magnitude)
orientation_bin_list.append((gradient_orientation-angle)*bins_per_degree)
for row_bin,col_bin,magnitude,orientation_bin in zip(row_bin_list,col_bin_list,magnitude_list,orientation_bin_list):
row_bin_floor,col_bin_floor,orientation_bin_floor = floor([row_bin,col_bin,orientation_bin]).astype(int)
row_fraction,col_fraction,orientation_fraction = row_bin-row_bin_floor,col_bin-col_bin_floor,orientation_bin-orientation_bin_floor
if orientation_bin_floor < 0:
orientation_bin_floor += num_bins
if orientation_bin_floor >= num_bins:
orientation_bin_floor -= num_bins
c1 = magnitude * row_fraction
c0 = magnitude * (1-row_fraction)
c11 = c1 * col_fraction
c10 = c1 *(1-col_fraction)
c01 = c0 * col_fraction
c00 = c0 * (1-col_fraction)
c111 = c11 * orientation_fraction
c110 = c11 * (1- orientation_fraction)
c101 = c10 * orientation_fraction
c100 = c10 * (1-orientation_fraction)
c011 = c01 * orientation_fraction
c010 = c01 * (1 - orientation_fraction)
c001 = c00 * orientation_fraction
c000 = c00 * (1-orientation_fraction)
histogram_tensor[row_bin_floor+1,col_bin_floor+1,orientation_bin_floor] += c000
histogram_tensor[row_bin_floor+1,col_bin_floor+1,(orientation_bin_floor+1)%num_bins] += c001
histogram_tensor[row_bin_floor+1,col_bin_floor+2,orientation_bin_floor] += c010
histogram_tensor[row_bin_floor+1,col_bin_floor+2,(orientation_bin_floor+1)%num_bins] += c011
histogram_tensor[row_bin_floor+2,col_bin_floor+1,orientation_bin_floor]+=c100
histogram_tensor[row_bin_floor+2,col_bin_floor+1,(orientation_bin_floor+1)%num_bins]+=c101
histogram_tensor[row_bin_floor+2,col_bin_floor+2,(orientation_bin_floor)]+=c110
histogram_tensor[row_bin_floor+2,col_bin_floor+2,(orientation_bin_floor+1)%num_bins] += c111
descriptor_vector = histogram_tensor[1:-1,1:-1].flatten()
threshold = norm(descriptor_vector)*descriptor_max_value
descriptor_vector[descriptor_vector>threshold] = threshold
descriptor_vector /= max(norm(descriptor_vector),float_tolerance)
descriptor_vector = round(512*descriptor_vector)
descriptor_vector[descriptor_vector<0] = 0
descriptor_vector[descriptor_vector>255] = 255
descriptors.append(descriptor_vector)
return array(descriptors,dtype='float32')
def unpackOctave(keypoint):
"""
Compute octave, layer, and scale from a keypoint
:param keypoint:
:return:
"""
octave = keypoint.octave & 255
layer = (keypoint.octave >> 8)&255
if octave >= 128:
octave = octave | -128
scale = 1 / float32(1 << octave) if octave >= 0 else float32(1 << -octave)
return octave,layer,scale
验证与应用
我们完整的实现了SIFT算法,需要注意的是,我们按照原文描述,更多的关注SIFT的实现细节,计算优化并不是本文的重点。故相对于CV2中提供的SIFT APIs,本文实现的SIFT在计算速度上存在一定不足。
模板匹配是CV领域一种常见的任务。可表述为输入两张图片,一张为查询图片,一张为场景图片,任务目标为在场景图片中查找查询图片并计算出两者的单应矩阵。
我们根据OpenCV’s template matching demo.,调用本文实现的SIFT函数来对SIFT的实现进行验证。
